Convolutions

In this section, you will learn about the following components in Spatial:

LineBuffer
ShiftRegister
LUT
Spatial Functions

Note that a large collection of Spatial applications can be found here.

Overview

Convolution is a common algorithm in linear algebra, machine learning, statistics, and many other domains. The tutorials in this section will demonstrate how to use the building blocks that Spatial provides to do convolutions.

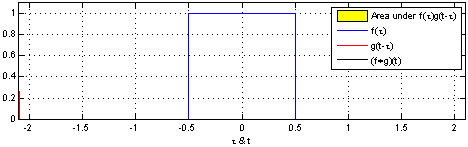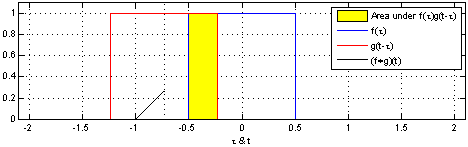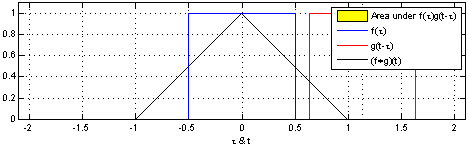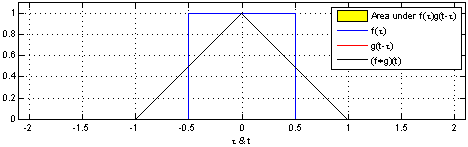
Specifically, we will build a basic differentiator for a time-series using sliding window averaging for an example 1D convolution. The animation to the right demonstrates this kind of 1D convolution with a square window kernel.

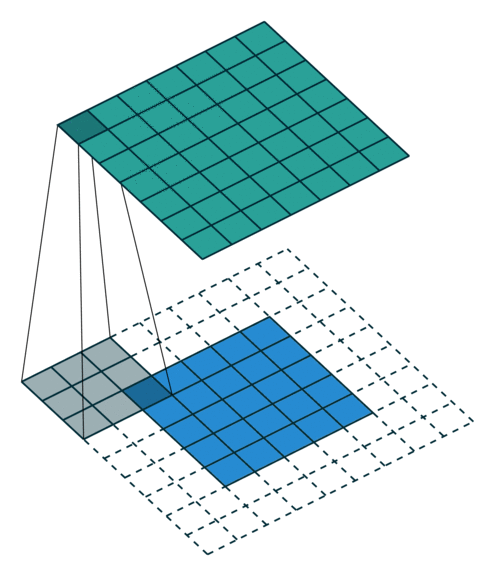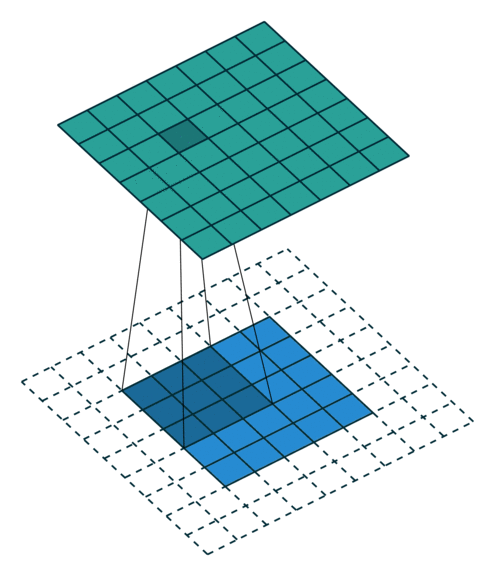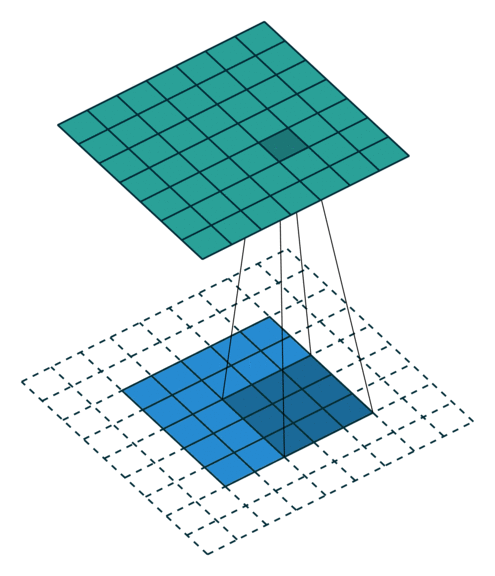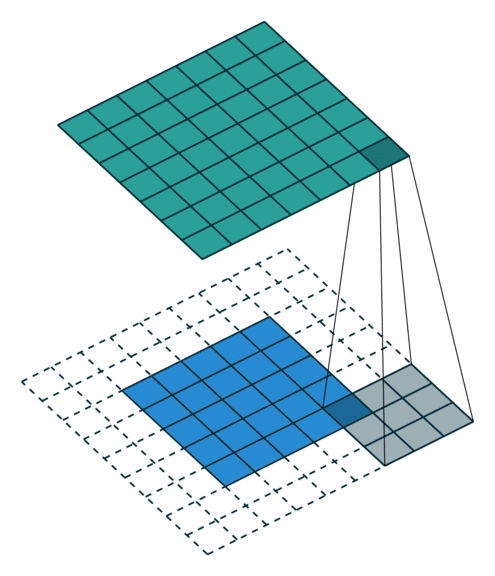
We will also build a 2D convolution application. The animation to the right demonstrates the 2D convolution with the padding that we will use (credit https://github.com/vdumoulin/conv_arithmetic). Alternatively, Spatial supports 2D convolutions as matrix multiplies. See (TODO: Link to “toeplitz” API) for more details.

Basic implementation (1D)

import spatial.dsl._

@spatial object Differentiator extends SpatialApp {

  def main(args: Array[String]): Unit = {
    type T = FixPt[TRUE,_16,_16]
    
    // Set tile size
    val coltile = 64
    
    // Load data
    val data = loadCSV1D[T](s"$DATA/slac/slacsample1d.csv", ",")
    
    // Set full size of input vector for use by FPGA
    val memcols = ArgIn[Int]
    setArg(memcols, data.length.to[Int])
    
    // Create input and output DRAMs
    val srcmem = DRAM[T](memcols)
    setMem(srcmem, data)
    val dstmem = DRAM[T](memcols)

    // Set low pass filter window size
    val window = 16

    Accel {
      // Create shift register window
      val sr = RegFile[T](window)
    
      // Allocate memories for input and output data
      val rawdata = SRAM[T](coltile)
      val results = SRAM[T](coltile)

      // Work tile by tile on input vector
      Foreach(memcols by coltile) { c =>
        
        // Fetch this tile
        rawdata load srcmem(c::c+coltile)
                                   
        // Scan through tile to get deriv
        Foreach(coltile by 1) { j =>
        
          // Shift next element into sliding window
          sr(*) <<= rawdata(j)
          
          // Compute mean of points in first half of window
          val mean_right = Reduce(Reg[T](0.to[T]))(window/2 by 1) { k => sr(0,k) }{_+_}
                               
          // Compute mean of points in second half of window
          val mean_left = Reduce(Reg[T](0.to[T]))(window/2 by 1) { k => sr(0,k+window/2) }{_+_}
                       
          // Subtract and average
          val slope = (mean_right - mean_left) / (window/2).to[T]
          
          // Store result (if all data in window is valid)
          val idx = j + c
          results(j) = mux(idx < window, 0.to[T], slope)
        }
        dstmem(c::c+coltile) store results
      }
    }


    // Extract results from accelerator
    val results = getMem(dstmem)

    // Read answer
    val gold = loadCSV1D[T](s"$DATA/slac/deriv_gold.csv", ",")

    // Create validation checks and debug code
    printArray(results, "Results:")
    val margin = 0.5.to[T]

    val cksum = gold.zip(results){case (a,b) => abs(a-b) < margin}.redu
 ce{_&&_}
    assert(cksum)
  }
}

In this example, we introduce a 1D convolution with one period of a square wave as the kernel. This is essentially a low pass filter and derivative of some input data. We will discuss the new syntax used in this app. To the right is a rough animation of what is happening in this app.

Spatial supports reading and writing to csv and binary files at runtime. Here, we have our data stored in a 1D csv file with , being the delimiter. The $DATA variable is substituted at the compile time of Spatial, and will use the environment variable on your system TEST_DATA_HOME. You may point this to wherever your data exists, or optionally clone our data repository if you are testing with our example code.

Here we create a shift register called sr. A RegFile in spatial is an N-dimensional addressable memory similar to an SRAM. The only difference is that the underlying resources used to create a RegFile are registers, while an SRAM will generally be placed in block RAM on an FPGA. A RegFile is an array of registers, which means it is inherently fully banked.

In order to support vectors of any size, we have tiled by coltile. We first fetch the tile we are working on, and then iterate element by element and shift the data into the RegFile. This shift operation pushes old data one address higher and puts the new data in address 0.

Rather than directly storing a kernel, we are using a square wave for this app. This means anything in the first half of the window is multiplied by -1 and anything in the second half is multiplied by 1. Therefore we can average the two halves separately and subtract one from the other to get the derivative.

For the first few iterations, the data in the RegFile will be uninitialized and could be any value, so we simply want to mask this out from the final result. As we step to new tiles, data from the previous tile will still exist in the RegFile, so we do not have to worry about masking it.

The graph to the right shows a plot of the input and expected output for this app.

To compile the app for a particular target, see the Targets page

Basic implementation (2d)

import spatial.dsl._

@spatial object Sobel extends SpatialApp {

  def main(args: Array[String]): Unit = {
    // Set up kernel height and width
    val Kh = 3
    val Kw = 3

    // Set max number of columns and pad size
    val Cmax = 160
    val pad = 3
    
    // Set up data for kernels
    val kh_data = List(List(1,2,1), List(0,0,0), List(-1,-2,-1))
    val kv_data = List(List(1,0,-1), List(2,0,-2), List(1,0,-1))

    val B = 16

    // Get image size from command line
    val r = args(0).to[Int]
    val c = args(1).to[Int]

    // Generate some input data
    val image = (0::r, 0::c){(i,j) => if (j > pad && j < r-pad && i > pad && i < r - pad) i*16 else 0}

    // Set args
    val R = ArgIn[Int]
    val C = ArgIn[Int]
    setArg(R, image.rows)
    setArg(C, image.cols)

    // Set up parallelization factors
    val lb_par = 16 (1 -> 1 -> 16)
    val par_store = 16
    val row_stride = 10 (100 -> 100 -> 500)
    val row_par = 2 (1 -> 1 -> 16)
    val par_Kh = 3 (1 -> 1 -> 3)
    val par_Kw = 3 (1 -> 1 -> 3)

    // Set up input and output images
    val img = DRAM[Int](R, C)
    val imgOut = DRAM[Int](R, C)

    // Transfer data to memory
    setMem(img, image)

    Accel {
      // Iterate over row tiles
      Foreach(R by row_stride par row_par){ rr =>

        // Handle edge case with number of rows to do in this tile
        val rows_todo = min(row_stride, R - rr)

        // Create line buffer, shift reg, and result
        val lb = LineBuffer[Int](Kh, Cmax)
        val sr = RegFile[Int](Kh, Kw)
        val lineOut = SRAM[Int](Cmax)

        // Use Scala lists defined above for populating LUT
        val kh = LUT[Int](3,3)(kh_data.flatten.map(_.to[Int]):_*)
        val kv = LUT[Int](3,3)(kv_data.flatten.map(_.to[Int]):_*)

        // Iterate over each row in tile
        Foreach(-2 until rows_todo) { r =>

          // Compute load address in larger image and load
          val ldaddr = if ((r+rr) < 0 || (r+rr) > R.value) 0 else {r+rr}
          lb load img(ldaddr, 0::C par lb_par)

          // Iterate over each column
          Foreach(0 until C) { c =>

            // Reset shift register
            Pipe{sr.reset(c == 0)}

            // Shift into 2D window
            Foreach(0 until Kh par Kh){i => sr(i, *) <<= lb(i, c) }

            val horz = Reduce(Reg[Int])(Kh by 1 par par_Kh, Kw by 1 par par_Kw){(i,j) =>
              sr(i,j) * kh(i,j)
            }{_+_}
            val vert = Reduce(Reg[Int])(Kh by 1 par par_Kh, Kw by 1 par par_Kw){(i,j) =>
              sr(i,j) * kv(i,j)
            }{_+_}

            // Store abs sum into answer memory
            lineOut(c) = mux(r + rr < 2 || r + rr >= R-2, 0.to[Int], abs(horz.value) + abs(vert.value))
          }

          // Only if current row is in-bounds, store result to output DRAM
          if (r+rr < R && r >= 0) imgOut(r+rr, 0::C par par_store) store lineOut
        }

      }
    }
    val output = getMatrix(imgOut)

    /*
      Filters:
      1   2   1
      0   0   0
     -1  -2  -1

      1   0  -1
      2   0  -2
      1   0  -1

    */
    // Compute gold check
    val gold = (0::R, 0::C){(i,j) =>
      if (i >= R-2) {
        0
      } else if (i >= 2 && j >= 2) {
        val px00 = image(i,j)
        val px01 = image(i,j-1)
        val px02 = image(i,j-2)
        val px10 = image(i-1,j)
        val px11 = image(i-1,j-1)
        val px12 = image(i-1,j-2)
        val px20 = image(i-2,j)
        val px21 = image(i-2,j-1)
        val px22 = image(i-2,j-2)
        abs(px00 * 1 + px01 * 2 + px02 * 1 - px20 * 1 - px21 * 2 - px22 * 1) + abs(px00 * 1 - px02 * 1 + px10 * 2 - px12 * 2 + px20 * 1 - px22 * 1)
      } else {
        0
      }
      // Shift result down by 2 and over by 2 because of the way accel is written
    }

    printMatrix(image, "Image")
    printMatrix(gold, "Gold")
    printMatrix(output, "Output")

    val cksum = gold == output
    println("PASS: " + cksum + " (Sobel)")
    assert(cksum)
  }
}

Here we show one of many ways to write a 2D convolution. Specifically, we are running a Sobel filter, which is roughly a simple edge detector in an image.

Here we set up the data for both kernels as Lists, which are not virtualized in Spatial. This means they are treated as Scala lists even at compile time of Spatial. This is one of many ways to use Scala to metaprogram Spatial.

Here we create image data in no particularly important way.

In this design, we tile by row, which allows us to use row_par to let the FPGA parallelize across multiple chunks of input data. We are careful here to handle the edge case, when there is fewer than a full tile of rows left in the loop.

Here we create a LineBuffer and a RegFile. The animation below shows how LineBuffers work. It is important to use LineBuffers correctly in their parent control structures, or else unexpected behavior may occur.

A LineBuffer is a general case of a buffered memory, where we can consistently index into rows 0 (newest data), 1, and 2 (oldest data), but have new rows loading in the background that will be pushed to row index 0 at the next buffer swap. In order to understand the swapping procedure, you should look at the least-common ancestor (LCA) of all the reads and writes to the memory. In this case, the LCA of the write and read for this LineBuffer is the loop Foreach(-2 until rows_todo). The first stage of this loop is the load into the LineBuffer, and the second stage is the Foreach(0 until C) loop which contains the read to the LineBuffer deeper in its sub-tree. There is a third stage to this controller, but it is irrelevant with respect to the operation of this LineBuffer.

The LineBuffer will swap its data on the exact cycle when all stages active during a particular iteration have received their done signals. This is the main reason why it is important to understand the control logic around the LineBuffer, or else it is possible to have unintended swapping behavior.

Here we shift 3 elements in parallel to each of the 3 rows of the sliding window. Note that it is entirely possible to perform this convolution without the intermediate RegFile, and the LineBuffer can be read directly. Using the intermediate RegFile just logically decouples the sliding window from the underlying memory.

Here we conditionally store our result back to DRAM as long as we are within valid bounds.

Using functions

import spatial.dsl._
@spatial object Differentiator extends SpatialApp {

  // Set low pass filter window size
  val window: scala.Int = 16

  def compute_kernel[T:Num](start: scala.Int, sr: RegFile1[T]): T = {
    Reduce(Reg[T](0.to[T]))(window/2 by 1) { k => sr(k+start) }{_+_} / window
  }

  def main(args: Array[String]): Unit = {
    type T = FixPt[TRUE,_16,_16]
    
    // Set tile size
    val coltile = 64
    
    // Load data
    val data = loadCSV1D[T](s"$DATA/slac/slacsample1d.csv", ",")
    
    // Set full size of input vector for use by FPGA
    val memcols = ArgIn[Int]
    setArg(memcols, data.length.to[Int])
    
    // Create input and output DRAMs
    val srcmem = DRAM[T](memcols)
    setMem(srcmem, data)
    val dstmem = DRAM[T](memcols)

    Accel {
      // Create shift register window
      val sr = RegFile[T](window)
    
      // Allocate memories for input and output data
      val rawdata = SRAM[T](coltile)
      val results = SRAM[T](coltile)

      // Work tile by tile on input vector
      Foreach(memcols by coltile) { c =>
        
        // Fetch this tile
        rawdata load srcmem(c::c+coltile)
                                   
        // Scan through tile to get deriv
        Foreach(coltile by 1) { j =>
        
          // Shift next element into sliding window
          sr <<= rawdata(j)
          
          // Compute mean of points in first half of window
          val mean_right = compute_kernel[T](0, sr)
                               
          // Compute mean of points in second half of window
          val mean_left = compute_kernel[T](window/2, sr)
                       
          // Subtract and average
          val slope = (mean_right - mean_left) / (window/2).to[T]
          
          // Store result (if all data in window is valid)
          val idx = j + c
          results(j) = mux(idx < window, 0.to[T], slope)
        }
        dstmem(c::c+coltile) store results
      }
    }


    // Extract results from accelerator
    val results = getMem(dstmem)

    // Read answer
    val gold = loadCSV1D[T](s"$DATA/slac/deriv_gold.csv", ",")

    // Create validation checks and debug code
    printArray(results, "Results:")
    val margin = 0.5.to[T]

    val cksum = gold.zip(results){case (a,b) => abs(a-b) < margin}.reduce{_&&_}
    assert(cksum)
  }
}

It is possible to separate code into different files and functions in Spatial. The code to the left demonstrates how to do this. Note that Spatial currently in-lines functions.

Previous: Matrix Multiply

next: genetic alignment