Inner Product
In this section, you will learn about the following components in Spatial:
Tiling
Reduce and Fold
Sequential execution and Coarse-grain pipelining
Parallelization
Basic buffering and banking
Note that a large collection of Spatial applications can be found here.
Overview
Inner product (also called dot product) is a basic linear algebra kernel, defined as the sum of the element-wise products between two vectors of data. For this example, we’ll assume that the data in this case are 32-bit signed fixed point numbers with 24 integer bits and 8 fractional bits. You could, however, also do the same operations with any type.
Basic implementation
import spatial.dsl._ @spatial object InnerProduct extends SpatialApp { def main(args: Array[String]): Void = { // Define data type type T = FixPt[TRUE,_24,_8] // Set vector length val len = 64 // Generate data val vec1 = Array.tabulate[T](len){i => i.to[T]} val vec2 = Array.tabulate[T](len){i => (len - i).to[T]} val d1 = DRAM[T](len) val d2 = DRAM[T](len) setMem(d1, vec1) setMem(d2, vec2) // Allocate reg for the answer val x = ArgOut[T] Accel { // Create local SRAMs val s1 = SRAM[T](len) val s2 = SRAM[T](len) // Transfer data s1 load d1 s2 load d2 // Multiply and accumulate x := Reduce(Reg[T](0))(len by 1){i => s1(i) * s2(i) }{_+_} } // Compute "correct" answer val gold = vec1.zip(vec2){_*_}.reduce{_+_} // Check answer assert(gold == getArg(x), r"Expected ${gold}, got ${getArg(x)}!") } }
Here we introduce the most basic implementation of vector inner product. In the next sections, we will use this example to demonstrate how to use Spatial’s API to build more efficient and complicated features into the app. First we will give a brief overview of the code to the left.
Note that we will use InnerProduct as an example to demonstrate how to improve the performance of your Spatial app in the Best Practices tutorial. The version shown in this tutorial is intended to demonstrate basic concepts in Spatial and is not the most optimized version.
In this implementation, we hardcode the length of the vectors. We use this size to set up the DRAMs and the SRAMs. We use Array.tabulate to create data for the vectors, as a function of the index, i.
We use the Reduce control structure to define a “map” function and a “reduce” function. Namely, these are s1(i) * s2(i) for the map function and addition as the reduce function. For more complicated reduce functions, it is possible to use the syntax {case (a,b) => f(a,b)} where function f can represent any function the user wants. The Reduce function also takes a Register as its first argument. In this case, we use Reg[T](0) to indicate that it should do its reduction into a new register of type T. It is also possible for us to use x directly as the reduction register, in which case it would read and write to the ArgOut for the reduction. Reduce then returns this register as its output. For no particular reason, we chose to use a new Reg for the reduction register and copy the value of this register to the ArgOut.
Below the Accel block, we write the code that computes the same function on the host so that we can check if the answer the FPGA provides is correct. You may inspect this code on your own to understand what it is doing.
To compile the app for a particular target, see the Targets page
tiling, Reduce, and fold
import spatial.dsl._ @spatial object InnerProduct extends SpatialApp { def main(args: Array[String]): Void = { type T = FixPt[TRUE,_24,_8] // *** Set tile size as compile-time constant val tileSize = 64 // *** Allow dynamically sized array val len = ArgIn[Int] setArg(len,args(0).to[Int]) // *** Use ArgIn to generate data and configure DRAM val vec1 = Array.tabulate[T](len){i => i.to[T]} val vec2 = Array.tabulate[T](len)[i => (len - i).to[T]] val d1 = DRAM[T](len) val d2 = DRAM[T](len) setMem(d1, vec1) setMem(d2, vec2) val x = ArgOut[T] Accel { // *** Create local SRAMs with fixed tile size val s1 = SRAM[T](tileSize) val s2 = SRAM[T](tileSize) // *** Loop over each tile x := Reduce(Reg[T](0))(len by tileSize){tile => s1 load d1(tile::tile+tileSize) s2 load d2(tile::tile+tileSize) // *** Return local accumulator to map function of outer Reduce Reduce(Reg[T])(0))(tileSize by 1){i => s1(i) * s2(i) }{_+_} }{_+_} } val gold = vec1.zip(vec2){_*_}.reduce{_+_} assert(gold == getArg(x), r"Expected ${gold}, got ${getArg(x)}!") } }
In most applications, there are some properties of the algorithm that are not known at compile time. Data structures may be dynamically sized and since it takes hours to synthesize for the FPGA, we will want to include as much flexibility for a given algorithm as possible.
The first way to incorporate flexibility is through “tiling.” This means we can allow data structures in the host to be dynamic while keeping properties in the Accel fixed. The rewrite of the application on the left shows what changes must be made to support tiling. Below we discuss these changes.
First, we must fix a tile size at compile time. In this example, we set it to 64. See the tutorial on DSE to learn how to auto-tune parameters like this. Next, we must expose the full vector size as an ArgIn to the FPGA. We set it with the first command line argument here.
When creating the data structures, we can use either the ArgIn or the command line args(0) interchangeably. Note that if you choose to use the ArgIn, you must set it before you can use it since this portion of the code is running on a CPU in sequential order. The default value for an ArgIn is 0 until this is overwritten.
Inside the Accel, we must add another loop that will loop over all of the tiles. Within a tile, we will run the same piece of code that was shown in the previous section. In the outer Reduce, we go over the entire length and our step size is the tile size. In local memory, we only fetch one tile at a time.
One thing that may be a little tricky at first is that the inner Reduce returns a scalar value in a register. This scalar value in a register is consumed by the outer Reduce as the result of its map function.
It is possible for the length of the vectors to not be divisible by the tile size. In this case, we would need to handle the edge case. There are two ways of doing so in this particular app. First, we can add a line inside the outer Reduce:
val actualTileSize = min(tileSize, len - tile)We could then use this in places instead of tileSize, as this would choose however many elements are left on the last iteration.
There is some hardware complexity associated with tile transfers whose sizes and bounds are not statically known. Another valid option would be to mask out values of the map function of the inner Reduce. Specifically, we could change the function to be:
mux(i + tile <= len, s1(i) * s2(i), 0.to[T])This way, as long as the global index for the element at-hand is within the range of the original vector, the map will return the product of two elements. For all other cases, it will return the value 0 cast as type T.
Finally, we can introduce the concept of Fold in this example. Fold is similar to Reduce, except it does not use the initial value of the accumulating register for the first iteration of a loop. In cases where you want to accumulate on top of a value that already exists in a register, you can use Fold. We can change the outer loop to Fold(x)(…){…}{…} without changing the result, since this Fold only runs once and x starts at 0 since it is an uninitialized arg. This is not a semantically useful example, but is simply another way to write this app.
Coarse-grain pipelining
import spatial.dsl._ @spatial object InnerProduct extends SpatialApp { def main(args: Array[String]): Void = { type T = FixPt[TRUE,_24,_8] val tileSize = 64 val len = ArgIn[Int] setArg(len,args(0).to[Int]) val vec1 = Array.tabulate[T](len){i => i.to[T]} val vec2 = Array.tabulate[T](len)[i => (len - i).to[T]] val d1 = DRAM[T](len) val d2 = DRAM[T](len) setMem(d1, vec1) setMem(d2, vec2) val x = ArgOut[T] Accel { val s1 = SRAM[T](tileSize) val s2 = SRAM[T](tileSize) // *** Enfore pipelined execution x := Pipe.Reduce(Reg[T](0))(len by tileSize){tile => s1 load d1(tile::tile+tileSize) s2 load d2(tile::tile+tileSize) // *** Enforce pipelined execution Pipe.Reduce(Reg[T])(0))(tileSize by 1){i => s1(i) * s2(i) }{_+_} }{_+_} } val gold = vec1.zip(vec2){_*_}.reduce{_+_} assert(gold == getArg(x), r"Expected ${gold}, got ${getArg(x)}!") } }
Sequenced execution
Pipelined execution
In the rewrite of the app in this section, you will notice two changes. We annotated the two Reduce loops with the Pipe tag. This enforces that they will run in a pipelined fashion and the compiler is not allowed to override this behavior. Without any annotation, the compiler will default to Pipe but may decide to use a different tag if DSE finds a more efficient design. We will now discuss how controllers are scheduled and what it means in the context of outer and inner controllers.
In Spatial, a controller is either an inner or an outer controller. To review the Control Flow tutorial,
Inner controllers contain only primitives (i.e.- arithmetic, memory access, muxing, etc.)
Outer controllers contain at least one other controller (i.e.-
Foreach,Reduce,FSM, etc.) and “transient” operations that do not consume FPGA resources (i.e.- bit slicing, struct concatenation, etc.)
In the example on the left, the outer Reduce contains two loads (which are substituted inside the compiler by a specific controller sub-tree to handle transactions to DRAM) and the other Reduce controller. This other Reduce is an inner controller because it consists of only a multiply operation, which is an arithmetic primitive.
We have added the annotation Pipe to both of these controllers, which broadly means that we want the compiler to use pipeline parallelism as much as possible for these controllers. In the outer controller, this means that the stages will execute in this manner:
Both loads will execute for in parallel tile = 0 (since they have no data dependencies). When they are both done, the Reduce will execute with tile = 0 while the loads will then execute with tile = 64, and so on. In software terminology, this particular case of coarse-grain pipelining is known as “prefetching,” but the concept can be generally applied in Spatial to overlap any operations with any other operations with any depth of pipeline.
Pipelining of outer controllers requires the compiler to insert N-buffered memories. In this particular example, both SRAMs will be double buffered so that data loading into the SRAM in the first stage of the controller does not overwrite data that is being read out of the SRAM in the second stage of the controller.
For the inner controller, this means that the hardware will issue a new value for i at each cycle. Even though the multiply operation may have a latency of 6 cycles, we could expect to get 6 new results in 6 cycles once the pipeline is running at steady-state. In more complicated examples, it is possible for loop-carry dependencies over the entire body or a subset of the body to appear, in which case the compiler would choose the initiation interval of the controller to ensure correctness.
In addition to Pipe, Spatial supports the annotations Sequenced and Stream.
Sequenced refers to no pipelining at all in outer controllers, and an initiation interval equal to the full latency of the body in inner controllers. With this annotation, a single value of a counter will propogate through all stages of a controller before it increments. While it is slower than Pipe, it consumes fewer resources and could be a solution to loop-carry dependency issues.
Stream refers to a control schedule that is pipelined at the data level. A two-stage pipeline annotated as a Stream controller means that any stage in the pipeline may execute as long as its input stream-style memories (FIFOs, DRAM Buses, etc.) have valid data and its output stream-style memories are ready to receive data. A more detailed discussion about these will be discussed later in the tutorial.
The animations to the left demonstrate the execution of this app with both Pipe and Sequenced tags.
parallelization
import spatial.dsl._ @spatial object InnerProduct extends SpatialApp { def main(args: Array[String]): Void = { type T = FixPt[TRUE,_24,_8] val tileSize = 64 val len = ArgIn[Int] setArg(len,args(0).to[Int]) val vec1 = Array.tabulate[T](len){i => i.to[T]} val vec2 = Array.tabulate[T](len)[i => (len - i).to[T]] val d1 = DRAM[T](len) val d2 = DRAM[T](len) setMem(d1, vec1) setMem(d2, vec2) val x = ArgOut[T] Accel { // *** Parallelize tile x := Reduce(Reg[T](0))(len by tileSize par 2){tile => // *** Declare SRAMs inside loop val s1 = SRAM[T](tileSize) val s2 = SRAM[T](tileSize) s1 load d1(tile::tile+tileSize) s2 load d2(tile::tile+tileSize) // *** Parallelize i Reduce(Reg[T])(0))(tileSize by 1 par 4){i => s1(i) * s2(i) }{_+_} }{_+_} } val gold = vec1.zip(vec2){_*_}.reduce{_+_} assert(gold == getArg(x), r"Expected ${gold}, got ${getArg(x)}!") } }
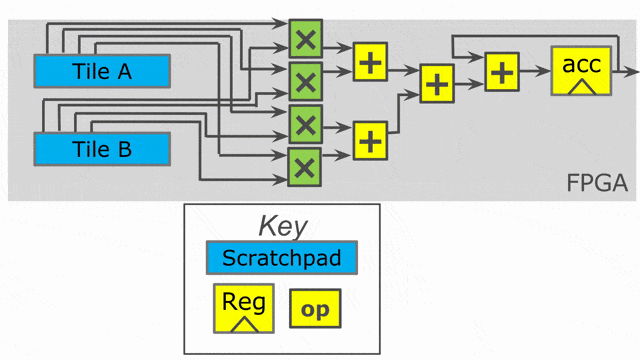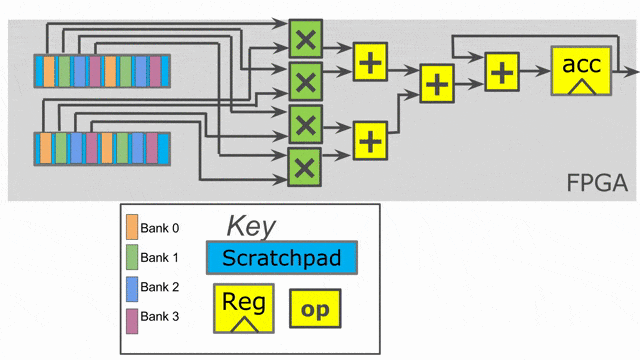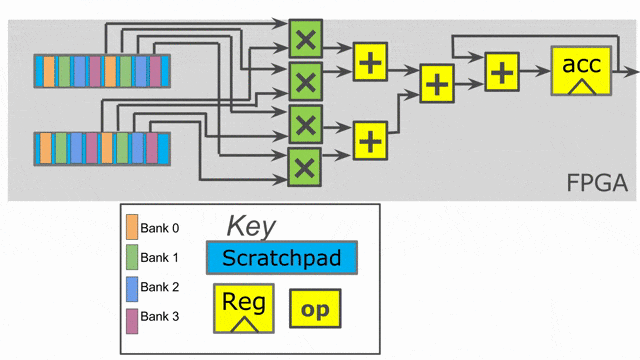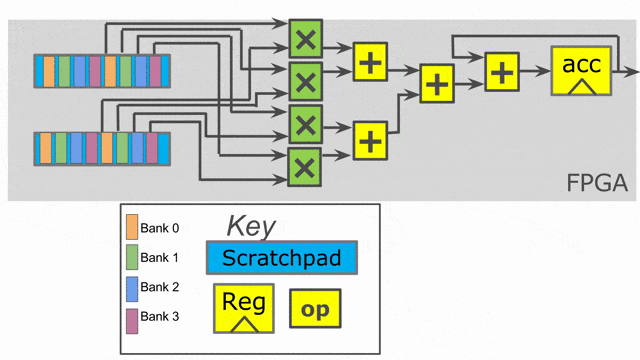
Inner parallelization
Outer parallelization
In this example, all we add are two parallelization annotations. We parallelize the outer loop by 2 and the inner loop by 4. When you use parallelization in Spatial, you should think of the associated iterator (in this case tile and i) as being vectorized by the parallelization factor. Rather than exhibiting one value at a time, the iterator will exhibit multiple consecutive values at the same time. This means on the first iteration of the outer loop, we will process tile = 0 and tile = 64 in parallel.
The compiler will unroll the outer loop by 2, which means it will duplicate whatever control structures are inside of it to provide the hardware to run in parallel. Note that we had to move the SRAM declarations to be inside this loop, as the compiler will also unroll memory declarations that exist inside of it. We need unique SRAMs for both lanes of this controller, so we want them to get unrolled with everything else.
The inner loop has a parallelization of 4, which means we will issue 4 elements into the map function at once (i.e.- i = 0, i = 1, i = 2, and i = 3), and a summing tree of depth log2(4) = 2 will be generated to accumulate all of the lanes with the shortest latency possible.
The animations show the hardware generated by this app with outer parallelization and inner parallelization (separately).